Dirichlet Process

Posted on August 16, 2016 )

Categories:

Lately I’m dealing with Bayesian non-parametric in order for the praparation of my next paper. Therefore, I spent several days trying to learn and understand Dirichlet process. Dirichlet process is at first difficult to understand, mainly because it is very different from our previous parametric methods and it uses advanced mathmetical concepts. I struggled several days to finally understand Dirichlet process. Once you understand it, it becomes very easy.

$G$ is a random probability measure. We say $G$ is Dirichlet process distributed with base distribution $H$ and concentration parameter $\alpha$, written $G \sim DP(\alpha,H)$ if

$$(G(A_1),...,G(A_r)) \sim Dir(\alpha H(A_1),...,\alpha H(A_r))$$

for every finite measure partition $A_1,…,A_r$ of $\Theta$.

In every tutorial and lecture, we are told that a sample from Dirichlet process is discrete and has point mass at atoms. In order to understand why this is that, it is important to know the posterior of Dirichlet process. Let $\theta_1,…,\theta_n$ be a sequence of independent draws from $G$. Let $n_k = \sharp\{i: \theta_i \in A_k\}$ be the number of observed values in $A_k$. From the conjugacy between the Dirichlet and multinomial, we have

$$(G(A_1),...,G(A_r))|\theta_1,...,\theta_n \sim Dir(\alpha H(A_1)+n_1,...,\alpha H(A_r)+n_r) \\ G|\theta_1,...\theta_n \sim DP(\alpha+n,\frac{\alpha}{\alpha+n}H+\frac{n}{\alpha+n}\frac{\sum_{i=1}^n \delta_{\theta_i}}{n})$$

Therefore, the posterior predictive given first $n$ observations is given by posterior of $G$, integrating out (i.e. the base distribution of posterior Dirichlet process):

$$\begin{aligned} P(\theta \in A | G,\theta_1,...,\theta_n) &= E[G(A)|\theta_1,...,\theta_n]\\ &= \frac{1}{\alpha+n}(\alpha H(A)+\sum_{i=1}^n \delta_{\theta_i}(A)) \end{aligned}$$

That is to say:

$$\theta_{n+1}|\theta_1,...,\theta_n \sim \frac{1}{\alpha+n}(\alpha H + \sum_{i=1}^n \delta_{\theta_i})$$

This in fact show that a sample from Dirichlet process has point masses located at the previous draws $\theta_1,…,\theta_n$. With positive probability, draws from G will take on the same value as previous seen observations. While it also has probability to draw from prior distribution $H$, smooth or not. With long enough sequence of draws from G, the value of any draw will be repeated by another draw, implying that $G$ is composed only of a weighted sum of point masses, i.e. it is a discrete distribution.

$$G = \sum_{k=1}^{\infty} \pi_k\delta_{\theta_k^*}$$

The above predictive in fact corresponds to MacQueen urn scheme and the above infinite sum corresponds to Stick-breaking construction. And the famous Chinese Restaurant Process is in fact very similar to MacQueen urn scheme except for different metaphor, both construction has rich-get-richer property. I don’t want to repeat the constructions here, but refer to Yee Whye Teh’s tutorial if necessary.

However, I do want to state the stick-breaking construction here since it would be useful for susequent Dirichlet Process Mixture Model. The stick-breaking construction separates the construction of $\pi$ and $\theta$. The construction of $\pi$ follows stick-breaking process

$$\beta_k \sim Beta(1,\alpha)\\ \pi_k = \beta_k \prod_{l=1}^{k-1}(1-\beta_k)$$

also written as $\pi \sim GEM(\alpha)$. And the $\theta_k^*$ is sampled directly from the base distribution:

$$\theta_k^* \sim H \\ G = \sum_{k=1}^{\infty} \pi_k \delta_{\theta_k^*}$$

DP Mixture Model

Intended to solve the $k$ selection problem for mixture model, LDA, etc, applying Dirichlet process to the problems serves to automatically select the number of mixture components or dimension of variables. Here, I’ll first investigate the application to DP Mixture model.

We model a set of observations $\{x_1,…,x_n\}$ using a set of latent parameters $\{\theta_1,…,\theta_n\}$. Each $\theta$ is drawn independently and identically from $G$, while each $x_i$ has distribution $F(\theta_i)$ parameterized by $\theta_i$:

$$x_i|\theta_i \sim F(\theta_i)\\ \theta_i|G \sim G\\ G|\alpha,H \sim DP(\alpha,H)$$

And since $G$ is discrete, multiple $\theta_i$’s can take on the same value simutaneously, therefore it can be viewed that $x_i$ with the same value of $\theta_i$ belong to the same cluster. The mixture perspective can be made more in agreement with the usual representation of mixture models using the stick-breaking construction equaivalently:

$$\pi|\alpha \sim GEM(\alpha)\\ z_i|\pi \sim Multi(\pi)\\ \theta_k^*|H \sim H\\ x_i|z_i,\{\theta_k^*\} \sim F(\theta_{z_i}^*)$$

The model is shown as follows.

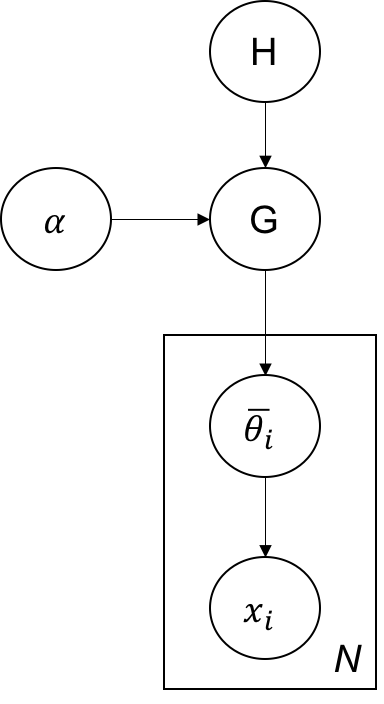
Solving the model using collapsed Gibbs sampling turns out to be very easy, as described in Murphy’s book p.886 (Algorithm 25.1). Before going through the algorithms, one should convince himself that the posterior predictive and prior predictive is easy for Gaussian distribution with conjugate prior as also talked in Murphy’s book in Chpater 4 and it should be Student-t distribution with the updated parameters (if I didn’t remember wrong). The key point is to compute this one

$$p(z_i=k|z_{-i},x,\alpha,\lambda) \propto p(z_i=k|z_{-i},\alpha)p(x_i|x_{-i},z_i=k,z_{-i},\lambda)$$

function dpm = dpm_gibbs(dpm,numiter);
% run numiter number of iterations of gibbs sampling in the DP mixture

KK = dpm.KK; % number of active clusters
NN = dpm.NN; % number of data items
aa = dpm.aa; % alpha parameter
qq = dpm.qq; % row cell vector of mixture components
xx = dpm.xx; % row cell vector of data items
zz = dpm.zz; % row vector of cluster indicator variables
nn = dpm.nn; % row vector of number of data items per cluster

for iter = 1:numiter
  % in each iteration, remove each data item from model, then add it back in
  % according to the conditional probabilities.

  for ii = 1:NN % iterate over data items ii

    % remove data item xx{ii} from component qq{kk}
    kk = zz(ii); % kk is current component that data item ii belongs to
    nn(kk) = nn(kk) - 1; % subtract from number of data items in component kk
    qq{kk} = delitem(qq{kk},xx{ii}); % subtract data item sufficient statistics

    % delete active component if it has become empty
    if nn(kk) == 0, 
      %fprintf(1,'del component %3d. K=%3d\n',find(nn==0),KK-sum(nn==0));
      KK = KK - 1;
      qq(kk) = [];
      nn(kk) = [];
      idx = find(zz>kk);
      zz(idx) = zz(idx) - 1;
    end

    % compute conditional probabilities pp(kk) of data item ii
    % belonging to each component kk
    % compute probabilities in log domain, then exponential
    pp = log([nn aa]);
    for kk = 1:KK+1
      pp(kk) = pp(kk) + logpredictive(qq{kk},xx{ii});
    end
    pp = exp(pp - max(pp)); % -max(p) for numerical stability
    pp = pp / sum(pp);

    % choose component kk by sampling from conditional probabitilies
    uu = rand;
    kk = 1+sum(uu>cumsum(pp));

    % instantiates a new active component if needed
    if kk == KK+1
      %fprintf(1,'add component %3d. K=%3d\n',kk,KK+1);
      KK = KK + 1;
      nn(kk) = 0;
      qq(kk+1) = qq(kk);
    end

    % add data item xx{ii} back into model (component qq{kk})
    zz(1,ii) = kk; 
    nn(1,kk) = nn(1,kk) + 1; % increment number of data items in component kk
    qq{1,kk} = additem(qq{1,kk},xx{ii}); % add sufficient stats of data item

  end
end

% save variables into dpm struct
dpm.qq = qq;
dpm.zz = zz;
dpm.nn = nn;
dpm.KK = KK;